数字电路: 锁存器/触发器的构造设计

在数字电路中, 只由逻辑门构成的组合电路本质上是不存储信息的, 它的输出会持续地响应输入的变化, 且只取决于输入的信息. 而在实现计算机的过程中, 我们知道图灵机是有状态且逐步转移的, 需要为我们所构造的计算机引入状态并在其中逐步转移, 为此我们需要引入能够记录状态并按顺序执行状态转移的元件, 也就是触发器 (flip-flop) / 锁存器 (latch) 与时钟. 这里记录一下各种锁存器/触发器的功能与结构.
锁存器 (latch)
锁存器本质上是一个双稳态电路, 它可以稳定在两个不同状态并在适当的输入下切换至另一个稳态. 而它处于哪个稳态就是我们要存储的信息.
SR 锁存器
SR 锁存器又称 RS 锁存器, 全称 set-reset latch, 直译为设置/重设锁存器. 它的功能很简单, 它有两个输入 $R$ / $S$ 和两个输出 $Q$ 和 $\overline{Q}$. 注意到这里的 $Q$ 指的是同一个值, 也就是说它的输出必定是互反的. 其中输入 $S$ 中输入 1 可以将 $Q$ 设置为 1, 而 $R$ 中输入 1 则可以将 $Q$ 重设为 0. 当 $S$ 和 $R$ 均为 0 时, $Q$ 保持其值. 而且 $S$ 和 $R$ 不能同时为 1. 其状态转移表如下:
| $S$ | $R$ | $Q_{next}$ | 转移 |
|---|---|---|---|
| 0 | 0 | $Q$ | 保持状态 |
| 0 | 1 | 0 | 重置为0 |
| 1 | 0 | 1 | 设置为1 |
| 1 | 1 | X | 非法状态 |
根据其使用的逻辑门种类有两种常见具体实现, 其中一种实现使用一对 NOR 门:
假设初始时 $Q=0$, 那么上方连结点处于低电平, 下方连结点处于高电平. 当 $R$ 和 $S$ 都是 0 时, 高电平作为 $R$ 侧 NOR 门的输入会导致上方连结点继续处于低电平; 而上方连结点的低电平作为 $S$ 侧 NOR 门的输入, 与 $S=0$ 运算后得到的 NOR 结果为 0, 可知下方连结点处继续处于高电平, 电路处于稳态. 这时的锁存器本质上相当于两个非门构成的环. 而 $Q=1$ 时是上述情况的对称.
当 $S=1$ 时, $S$ 侧的 NOR 门由于其中一个输入为 1 导致输出立刻变为 0, $\overline{Q}$ 输出变为 0. 同时输出信号传播到 $R$ 侧的 NOR 门, 因为此时 $R=0$, 运算得到的结果为 1, $Q$ 输出变为 1. 这个高电平信号传播回 $S$ 侧的 NOR 门, 使其输出保持为 0, 锁存器进入 $Q=1$ 的稳态.
当 $R=1$ 时, 情况与上述对称, 不同的是 $\overline{Q}$ 一侧变成高电平的一方.
当 $S=R=1$ 时, 两个 NOR 门都给出低电平输出, $Q \neq \overline{Q}$, 电路状态被打破. 一般情况下 SR 锁存器不应当处于这个状态.
与此对偶的还有用 NAND 门构造的 $\overline{SR}$ 锁存器, 结构如下:
注意到所有的输入/输出值都与 NOR 门构造的 SR 锁存器互非, 且在 $S=R=1$ 时两个输出均为高电平.
还有一种用 AND 和 OR 门构造的 SR 锁存器, 结构如下:
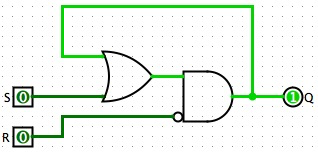
注意到这个锁存器只有一个 $Q$ 输出而没有 $\overline{Q}$ 输出. 其转移表与上面的 SR 锁存器有些微差异:
| $S$ | $R$ | $Q_{next}$ | 转移 |
|---|---|---|---|
| 0 | 0 | $Q$ | 保持状态 |
| 1 | 0 | 1 | 设置为1 |
| X | 1 | 0 | 重置为0 |
不同之处在于 $R=1$ 时不管 $S$ 的值如何, $Q$ 总是被重置为 0.
SR 锁存器作为一种最基本的锁存器, 可以作为其他锁存器/触发器的设计基础. 它拥有自己的符号, 如下图是 SR NAND 锁存器的符号:

JK 锁存器
JK 锁存器与 SR 锁存器类似, 也具有与 $S$ 和 $R$ 对应的 $J$, $K$ 输入与 $Q$ 输出, 但不同的是 JK 锁存器允许 $J=K=1$, 此时与 SR 锁存器不同的是会将 $Q$ 置为 $\overline{Q}$.
实现方法也很简单, 只需要在输入端再把 $Q$ 值做一次馈送, 令 $S=J\overline{Q}$, $R=KQ$ 即可. 容易发现 $S$ 和 $R$ 表达式中互非的项可以保证 $S$ 和 $R$ 不同时为 1 且在 $J=K=1$ 时选择 $S$ 和 $R$ 中合适的一个输入置为 1 来让 SR 锁存器的状态翻转.
但是 JK 锁存器由于没有时钟信号指导翻转操作而很少被使用. 当 $J=K=1$ 时, JK 锁存器实际上会变成一个振荡器. 其具体转移表如下:
| $J$ | $K$ | $Q_{next}$ | 转移 |
|---|---|---|---|
| 0 | 0 | $Q$ | 保持状态 |
| 0 | 1 | 0 | 重置为0 |
| 1 | 0 | 1 | 设置为1 |
| 1 | 1 | $\overline{Q}$ | 翻转输出 |
门控 SR 锁存器
普通的锁存器是 “透明的”, 也就是说输入信号的改变会立即体现在输出上. 我们可以添加一些其他逻辑门来让锁存器 “条件透明”, 也就是只有在某个控制输入信号 (enable 信号 $E$ , 或称 control 信号 $C$ ) 为 1 时才对 $S$ 和 $R$ 的输入作出响应. 这种锁存器被叫做门控锁存器, 也可以被叫做同步锁存器 (因为可以将 $E$ 接在时钟脉冲上来和其它元件同步) 实现上也非常简单, 我们只需要像 MUX 一样添加一层 AND 或者 NAND 门即可. 如下两图分别绘出了 SR NOR 锁存器与 SR NAND 锁存器的门控结构:


可以看到, 在 $E=0$ 时提供给 SR 锁存器的输入都被置为 0, 锁存器不对外部的 $S$ 和 $R$ 输入作出任何响应. 而当 $E=1$ 时, 门控锁存器的输入被原样提供给内部的 SR 锁存器, 锁存器根据外部的 $S$ 和 $R$ 输入产生相应的转移动作.
门控 SR 锁存器也有自己的符号, 如下图:

门控 D 锁存器
D 锁存器中的 D 指的是 data, 基于 SR 锁存器设计. 它的主要思想是分离数据信号 $D$ 和控制信号 $E$. 在 SR 锁存器中, 为了将输出设置为 0/1 时必须将两个输入中的特定一个置为 1, 而不能做到复制某个传送过来的数据. 而 D 锁存器通过在 SR 锁存器的基础上添加运算逻辑, 抽象出数据输入和控制输入, 令锁存器在控制信号置为 1 时将数据信号的状态复制到锁存器中. 这种锁存器更符合为寄存器赋值时的思维方式, 得到广泛应用. 它的具体结构如下:

容易看出右半部分就是一个 NAND 构造的 SR 锁存器. 而左半部分可以被当做一个 “翻译层”, 将 $D$ 和 $E$ 的输入转换为 $S$ 和 $R$ 信号传递给 SR 锁存器. 它的状态转移表如下:
| $E$ | $D$ | $Q_{next}$ | 转移 |
|---|---|---|---|
| 0 | X | $Q$ | 保持状态 |
| 1 | 0 | 0 | 写入0 |
| 1 | 1 | 1 | 写入1 |
当 $E=0$ 时, 容易看出左侧两个 NAND 门的输出都一定被置为 1, 也就是说 $\overline{S}=\overline{R}=1$, 即 $S=R=0$.
当 $E=1$ 时, 如果 $D=0$, 则上方 NAND 门的输入仍有一个为 0, 输出 $\overline{DE}$ 为 1, 即 $\overline{S}=1$, $S=0$. 同时这个输出被传递给下方 NAND 门, 下方 NAND 门两个输入 $E$ 和 $\overline{DE}$ 均为 1, 输出 $\overline{E\overline{DE}}$ 为 0, 即 $\overline{R}=0$, $R=1$.
而如果 $E=D=1$, 则 $\overline{S}=\overline{DE}=0$, $S=1$. 而 $\overline{R}=\overline{E\overline{DE}}=1$, $R=0$.
此处的两个 NAND 门的设计理由可以解释为, 它们都作为 “条件非门” 使用, 在 $E=1$ 时它们都是 $D$ 后连接的非门, 用来产生两个互非的信号. 而当 $E=0$ 时则不受 $D$ 影响.
Earle 锁存器
D 锁存器有一个缺陷, 就是它在不同的情形下可能走过 2 个或 3 个门延迟, 使得它延迟不定而可能产生逻辑冒险 (hazard). 而 Earle 锁存器通过引入一个 $\overline{E}$ 输入使得它能够在任意情况下输出都耗费 2 个门延迟. 它的结构如下:

其中 $E_H$ 为高电平控制信号, 即 $E$. 而 $E_L$ 为低电平控制信号, 即 $\overline{E}$. 这两个信号可以同时被时钟元件产生所以没有延迟, 容易发现任意输入的改变都刚好传播 2 个 NAND 门后到达 $Q$. 它的真值表与 D 触发器完全一样, 因为可以避免逻辑冒险也被广泛使用.
触发器 (flip-flop)
触发器类似受到时钟控制的锁存器, 其中有一个输入被连接到同步的时钟, 并且触发器在特定时钟时刻会对输入有不同的响应.
D 触发器
D 触发器可以捕捉时钟信号的某个特定时刻 (比如上升沿) 并将输出值设置为输入 $D$. 在其他时刻, 输出 $Q$ 不变. D 触发器可以被看作一个存储单元, 一个零阶保持器 (zero-order hold) 或者一个推迟器 (delay line). 许多 D 触发器除了时钟信号输入和 $D$ 作为输入之外还接受 $S$ 和 $R$ 两个输入, 功能与 SR 锁存器一致, 用来在忽略时钟限制与 $D$ 输入的情况下强制将触发器的输出设置为 1 或重设为 0. D 触发器可以作为许多电子设备的关键基础部件, 比如 D 触发器阵列组成的移位寄存器可以在设备中用于将信号在串行和并行之间转换 (比如将总线输入每 clock 一位地逐位读出) 或者作为串行 buffer.
D 触发器有自己的符号, 其中 > 为时钟输入. $S$ 和 $R$ 在不需要的时候可以省略.

经典 D 触发器
上升沿 D 触发器顾名思义, 会在时钟上升沿将 $Q$ 设置为 $D$. 注意到这个和门控 D 锁存器有一个明显的区别, 就是门控 D 锁存器只要在 $E$ 为 1 的时候就会持续响应 $D$ 的变化, 而上升沿 D 触发器则只在上升沿时刻接受 $D$ 的输入状态, 而在剩余的时钟信号高电平时不对 $D$ 的变化产生响应. 上升沿 D 触发器的结构如下:

我们可以看到整个电路由 3 个 SR NAND 锁存器构成. 结构上类似将 D 锁存器左侧的两个 NAND 门换成 SR 锁存器. 这两个锁存器的作用可以被认为是"锁定"产生低电平的输出. 输入侧的两个 SR 锁存器将和下游连接的输出部分看做 $Q$, 时钟信号一侧的输入看做 $\overline{S}$. 下方的 SR 锁存器将数据输入看做 $\overline{R}$. 上方锁存器的 $\overline{R}$ 输入可以看做下方锁存器的 $\overline{Q}$ 输出, 但后续我们会看到左侧的锁存器会有两个输入都是 0 的非法状况会需要具体分析.
当时钟信号为低电平时, 两个输入锁存器都被设置为 1, 下游输出锁存器的输入都是高电平, 输出锁存器保持其值. 此时如果数据信号是1, 则下方锁存器处于正常的设置状态. 但下方锁存器的 $\overline{Q}$ 作为上方锁存器的 $\overline{S}$ 输入, 上方锁存器 $\overline{S}=\overline{R}=0$, 两个输出都是高电平. 而当数据信号是 0, 下方锁存器就处于非法状态, 两个输出都是 1, 而上方锁存器处于正常的被设置为 1 的状态.
此时, 处于非法状态一侧的锁存器就是要在上升沿向下游输出低电平的锁存器.
当时钟信号处于上升沿的时候, 非法一侧的锁存器立刻处于正常的重设动作状态, 向对应侧的下游输出低电平. 根据上文分析, 数据信号是 1 时上方锁存器非法, 上升沿时上方锁存器向下游输出低电平, 对应 $\overline{S}=0$, 输出锁存器被置为 $Q=1$. 同理当数据信号是 0 时, 输出锁存器被置为 $Q=0$.
当时钟信号继续处于高电平时, 输出锁存器不应该继续受到数据输入的影响. 首先假设上升沿数据输入是 0, 根据上文推断下方的锁存器向下游输出低电平, 那么下方锁存器实际上处于重设动作状态. Data 输入不管是 0 还是 1 都会让这个锁存器继续向下游输出 0. 而上方的锁存器的两个输入一直保持高电平, 处于保持状态. 而如果上升沿数据输入是 1, 则上方的锁存器向下游输出低电平. 这时注意, 中间将上方锁存器输出连向下方锁存器的时钟侧输入的连线会向 NAND 门引入一个低电平信号, 等价于将时钟输出设置为了 0. 此时下方锁存器要么处于非法状态, 要么处于设置为 1 的动作, 无论处于哪种状态都会向下游输出高电平. 而上方锁存器和数据输入为 0 的情况一样, 处于只能重设/保持两种动作, 无论是哪种都会让输出继续保持为低电平.
当时钟信号处于下降沿, 两个锁存器都立刻处于重设动作或非法状态, 两种都会向下游输出高电平, 输出锁存器的值继续保持.
主从 D 触发器
主从 D 触发器的工作原理比经典上升沿触发器好理解一些. 它把两个门控 D 锁存器串联来得到边沿触发的结果. 下降沿触发的主从 D 触发器结构如下:

它的工作原理十分简单, 输入侧的主 D 锁存器起到一个 “缓冲” 的作用, 在时钟信号高电平的时候一直令 $Q_M=D$, 从 D 锁存器则由于 $E$ 为低电平而忽略 $Q_M$ 的变化保持其原值. 而当时钟信号处于下降沿时, 主 D 锁存器不再变化, $Q_M$ 保持下降沿时 $D$ 的值. 与此同时, 从 D 锁存器的 $E$ 输入转为高电平, 指示它读取 $Q_M$ 的值并将其设置为输出.
而上升沿触发的版本在展开成门电路之后结构如下:

从中可以清晰地看到主/从两个门控 D 锁存器.
双边 D 触发器
双边 D 触发器在上升沿和下降沿都将自己的输出赋为 $D$. 具体实现可以直接用两个 D 锁存器和一个选择器, 如下图所示.
在图示里, 上方的锁存器中 $E=\overline{C}$, 在时钟低电平时保持 $Q=D$ 并在时钟上升沿与高电平时锁定保持. 下方的锁存器中 $E=C$, 在时钟高电平时保持 $Q=D$ 并在下降沿与低电平时锁定保持. 选择器在时钟高电平时选择上方锁存器的输出, 低电平时选择下方锁存器, 即可实现在上升沿/下降沿都触发保存.
JK 触发器
JK 触发器与 JK 锁存器类似, 但仅在时钟边沿响应输入. JK 触发器也像 D 触发器一样有多种实现结构, 一种理解起来比较简单的是主从结构. 下面是下降沿JK触发器的电路结构:
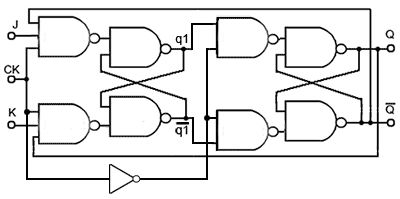
当时钟在高电平时, 左侧的主 SR 锁存器暂存 $S=J\overline{Q}$ 和 $R=KQ$ 的结果, 右侧的从 SR 锁存器保持 $Q$ 的值不被修改. 当时钟处于下降沿时以及低电平, 左侧的主 SR 锁存器的输入均为高电平, 本质上处于锁定状态, 将下降沿时刻计算得的 $S$ 和 $R$ 结果传递给下游的从锁存器, 从锁存器产生动作更新 $Q$ 的值.
除此之外, 也可以在 D 触发器的基础上实现 JK 触发器. 按照上文中 JK 锁存器的真值表, 我们可以进行如下化简:
构造出相应的门电路算出 $D$ 然后喂给 D 触发器就好了.
T 触发器
T 触发器中的 T 指的是 toggle. 它拥有输入 $T$ 和时钟信号输入. 当触发器触发的时候, 如果 $T=1$, 那么令 $Q_{next}=\overline{Q}$. 否则 $Q$ 保持不变. 以上升沿触发为例, 真值表如下:
| $T$ | 时钟 | $Q_{next}$ | 动作 |
|---|---|---|---|
| X | 非上升沿 | $Q$ | 保持 |
| 0 | 上升沿 | $Q$ | 保持 |
| 1 | 上升沿 | $\overline{Q}$ | 翻转 |
实现上有了 JK 触发器之后, 可以直接将 $T$ 同时连接到 JK 触发器的 $J$ 和 $K$ 输入即可实现上述功能.
参考资料
- Flip-flop (electronics) - Wikipedia
- JK Flip-flops, learnabout-electronics.org
- Multiplexer - Wikipedia
- 数字电子技术基础简明教程, 余孟尝
